The Zero-Product Property
Overview: In this lesson you will learn about the zero-product property and how to solve an equation using it.
Zero - Product Property Definition of Zero - Product Property
ab = 0
(or another set of variables=0)
than either
a=0 and/or b=0
because there's no other way the product could give zero.
So if we can write a quadratic equation as a couple of factors giving zero, then we can set each of those factors equal to zero and solve them independently to find the solutions to the original equation!
- Zero - Product Property states that if the product of two factors is zero, then at least one of the factors must be zero.
ab = 0
(or another set of variables=0)
than either
a=0 and/or b=0
because there's no other way the product could give zero.
So if we can write a quadratic equation as a couple of factors giving zero, then we can set each of those factors equal to zero and solve them independently to find the solutions to the original equation!
Examples of Zero - Product Property
Answer Choices:
Outer
Inner
Last
- If xy = 0, then x = 0 and/or y = 0.
Answer Choices:
- A. – 1, 5
- B. 1, 5
- C. – 5, - 1
- D. 1, - 5
Outer
Inner
Last
Step one
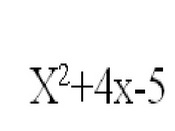
[Write out the entire problem]
Step 2: (x + 5)(x – 1) = 0 [Turn into 2 separate equations by using FOIL backwards: 5-1, 5x, x1, xx]
Step 4: x + 5 – 5 = 0 – 5 or x – 1 + 1 = 0 + 1 [Simplify the equations.]
Step 5: x = - 5 or x = 1
Step 6: The solutions for the equation (x + 5)(x – 1) = 0 are 1 and – 5.
The correct answer is: D 1,-5
- ( 5)( - 1)
- ( 5)(x - 1)
- (x + 5)( x - 1)
- (x + 5)(x - 1)
Step 4: x + 5 – 5 = 0 – 5 or x – 1 + 1 = 0 + 1 [Simplify the equations.]
Step 5: x = - 5 or x = 1
Step 6: The solutions for the equation (x + 5)(x – 1) = 0 are 1 and – 5.
The correct answer is: D 1,-5
All problems/information comes directly from: http://www.northstarmath.com/sitemap/zero-productproperty.html
Also information from: http://answers.yahoo.com/question/index?qid=20100425213028AAysXLl, from Answerer 1
I do not own any of this information. Thanks reliable resources, I want to give you credit for being so smart!
Also information from: http://answers.yahoo.com/question/index?qid=20100425213028AAysXLl, from Answerer 1
I do not own any of this information. Thanks reliable resources, I want to give you credit for being so smart!
