Exponents and Exponential Functions
What does a function look like?
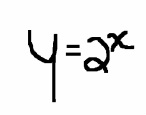
This is a very simple function.
The function reads as "y equals 2 to the x power"
The function reads as "y equals 2 to the x power"
Exponent Refresher:
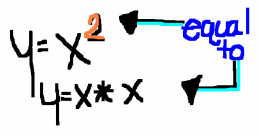
That equation tells you how to multiply x to get y.
If we want to find y when x=3, we can pretty quickly find that y=3*3=9. But, this is actually what's known as a "power function". In fact, it's just a polynomial, and not an exponential function at all.
Take a closer look at x2 . This means x squared or x to the second power. What does it mean?
We have two parts here:
1) An exponent, which is the number 2.
2) A base, which is the variable x.
With exponential functions, the variable will actually be the exponent, with a constant as the base.
If we want to find y when x=3, we can pretty quickly find that y=3*3=9. But, this is actually what's known as a "power function". In fact, it's just a polynomial, and not an exponential function at all.
Take a closer look at x2 . This means x squared or x to the second power. What does it mean?
We have two parts here:
1) An exponent, which is the number 2.
2) A base, which is the variable x.
With exponential functions, the variable will actually be the exponent, with a constant as the base.
Exponential Functions:
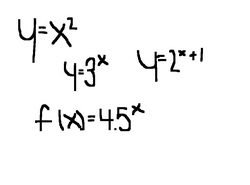
The eqation is y equals 2 raised to the x power. This sort of equations represents what we call " exponential growth" or "exonential decay". In the picture shows examples of other functions.
The general exponential function looks like this: , where the base b is any positive constant. The base b could be 1, but remember that 1 to any power is just 1, so it's a particularly boring exponential function.
The general exponential function looks like this: , where the base b is any positive constant. The base b could be 1, but remember that 1 to any power is just 1, so it's a particularly boring exponential function.
Examples:
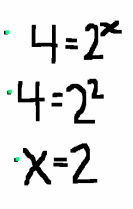
Solve for x: 4= 2x
This one is actually pretty simple, so let's just think it through:
The problem says we have to multiply x number of two's together to get four. Well, everyone knows that 2*2=4, so the answer is two:
This one is actually pretty simple, so let's just think it through:
The problem says we have to multiply x number of two's together to get four. Well, everyone knows that 2*2=4, so the answer is two:
What about a word problem example?
We can use a formula for exponential growth to model the population of a bacteria. Let's say the bacteria population is defined by B (T)= 100* 1.12t where B is the total population and t represents time in hours. While that may look complicated, it really tells us that the bacteria grows by 12 percent every hour. Every time another hour goes by, t goes up by 1, so we have to multiply the population times 1.12 again. The 100 simply sets the initial population at time t=0.
So, how much bacteria remains after 4 hours?
What do we know? We have the formula and the fact that t=4.
Replace t with 4 hours in the formula above and simplify.
We can use a formula for exponential growth to model the population of a bacteria. Let's say the bacteria population is defined by B (T)= 100* 1.12t where B is the total population and t represents time in hours. While that may look complicated, it really tells us that the bacteria grows by 12 percent every hour. Every time another hour goes by, t goes up by 1, so we have to multiply the population times 1.12 again. The 100 simply sets the initial population at time t=0.
So, how much bacteria remains after 4 hours?
What do we know? We have the formula and the fact that t=4.
Replace t with 4 hours in the formula above and simplify.
